B树
一、定义
B树是一个平衡的多路搜索树,每个节点可以存储多个元素。
二、性质
对于m阶B树(),设其任意节点存储元素的个数为x,那么:
- 对于根节点:
- 对于非根节点:
- 如果有子节点,子节点个数为
- 根节点子节点个数:
- 非根节点子节点个数:
举些例子:
- 当m=2时, 非根节点子节点个数:,故称为(1,2)树,就是二叉搜索树。
- 当m=3时, 非根节点子节点个数:,故称为(2,3)树。
- 当m=4时, 非根节点子节点个数:,故称为(2,4)树。
- 当m=5时, 非根节点子节点个数:,故称为(3,5)树。
数据库的应用中,一般使用200~300阶的B树
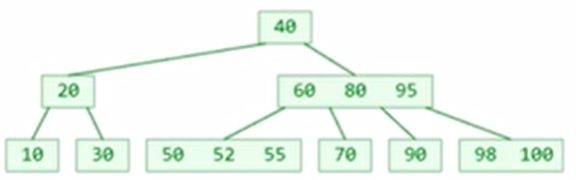
三、操作
1.搜索
同二叉搜索树一样,差不了多少,从根节点比大小,走分支
2.添加
同样也是比大小,走分支,最后走到叶子节点,比大小,找到合适的位置插入。 需要注意的是,添加只会发生在叶子节点上。
2.1.上溢
添加只会发生在叶子节点上,如果一直添加元素,当叶子节点元素个数等于m时,就违反了B树的定义。
因为无论是根节点还是非根节点,元素个数的上限都是。
上溢就是解决此问题的,当元素个数等于m时,选取当前节点中间位置的元素,将其送入父节点,与此同时被选中的元素的左元素们和右元素们都会成为该元素的子节点。
例如一个5阶B树,如下:
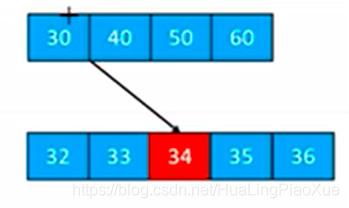
第2层有5个元素,大于4个,此时需要上溢。 选取中间元素34送入父节点
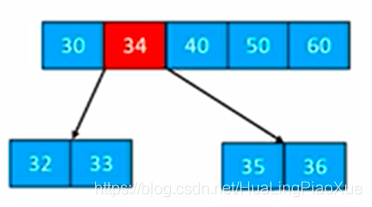
此时发现父节点元素个数也超过4了,继续上溢 选取中间元素40送入父节点
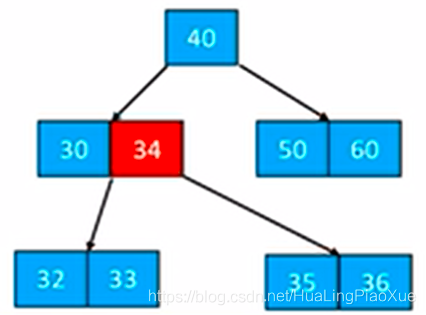
3.删除
当删除的节点为叶子节点时,直接删除即可
当删除的是非叶子节点时,需要找到该节点的前驱或后继,覆盖掉需要删除的节点。
例如:
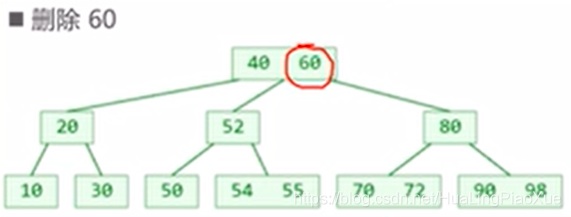
当要删除的时60时,找55或70覆盖掉60即可。 由此可以推出,删除引发的节点减少,最终会体现在叶子节点的减少上。
3.1.下溢
删除引发的节点减少,最终会体现在叶子节点的减少上。
如果一直删除元素,当叶子节点元素个数等于时,就违反了B树的定义。 因为无论是根节点还是非根节点,元素个数的下限都是。
下溢就是解决该问题的。当某个节点元素个数等于时,有两种情况。
相邻的兄弟节点至少有个元素 那么该节点可以与父节点、兄弟节点的元素进行交换。 举个例子:
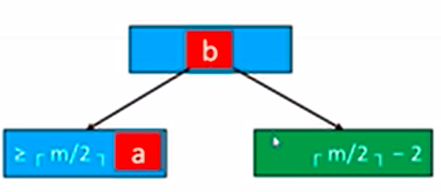
绿色节点元素个数,此时需要借一个元素。
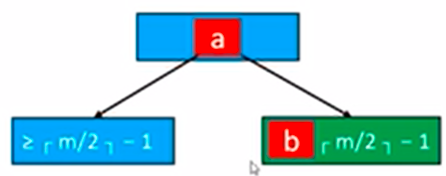
首先将a送入父节点,父节点的b送入绿色节点,此时绿色节点元素个数。这种操作也叫做旋转。
相邻的兄弟节点只有个元素 此时就不能用旋转的方法了,一旦使用旋转,兄弟节点也将违反约束。 该怎么办呢?只需将父节点的元素拿下来与两个子节点合并即可。 举个栗子:
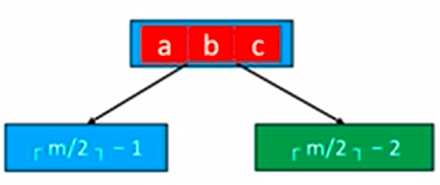
将父节点元素b拿下来合并。
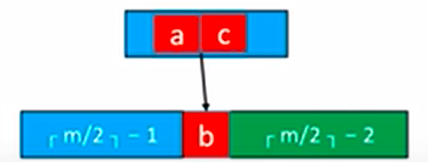
合并后的新节点元素个数为,必然不超过,也就是说合并后的新节点不会发生上溢。
