什么是连通分量

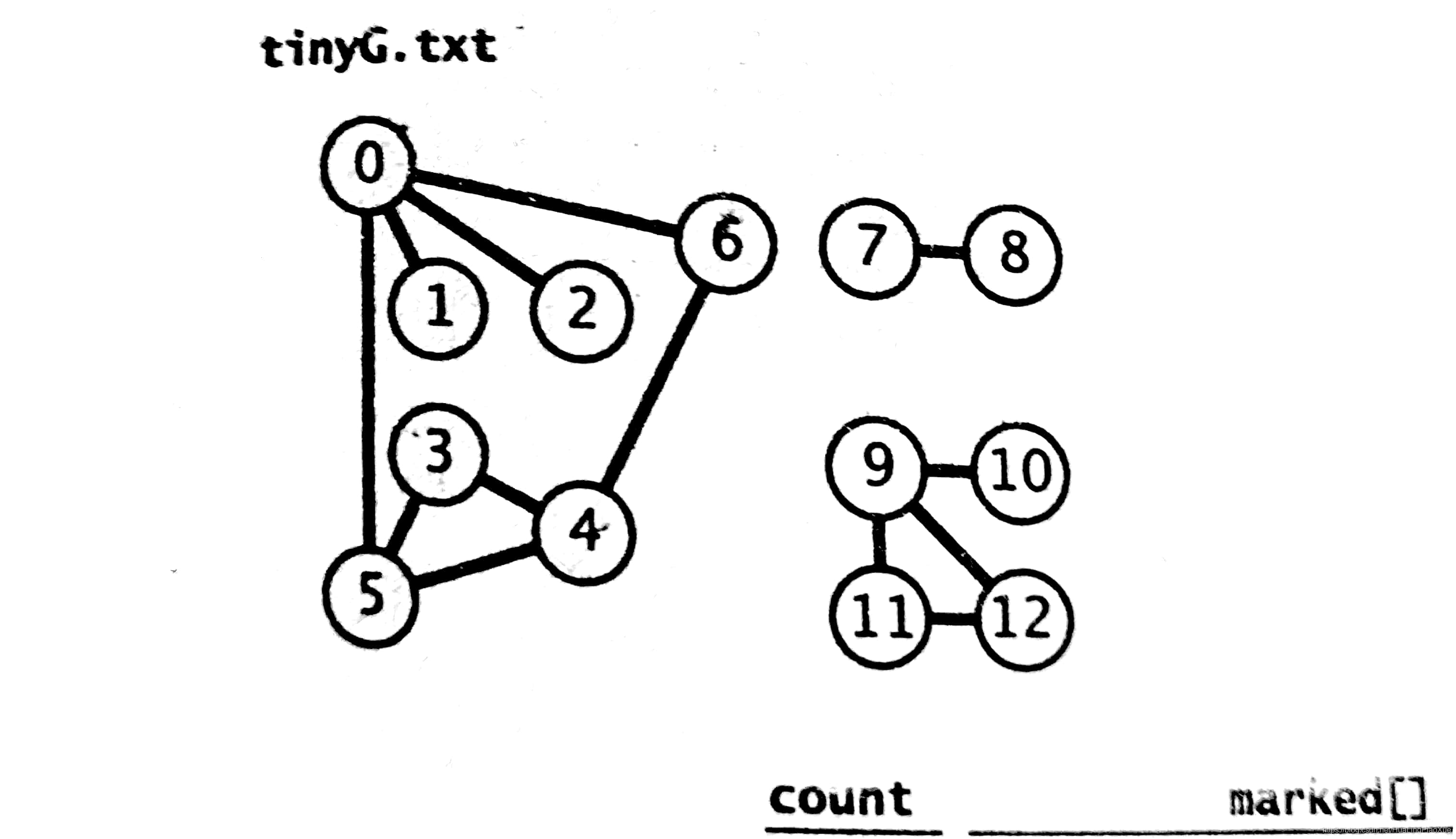
如图，在上面的图中有13个点，他们连接构成了三个部分。{0,1,2,6,3,4,5},{7,8},{9,10,11,12}这三个部分就是这个图的连通分量。

如何计算联通分量

使用dfs可以遍历一个点所在连通分量中所有的点。在每次遍历时，我们可以对一个连通分量中的点进行标记、染色。 例如： 首先，声明一个变量count用于统计，以及标记数组color[]。然后，从0开始遍历，我们会遍历完{0,1,2,6,3,4,5}连通分量，遍历过程中我们使用点的值作为索引为color[点]赋值为count。最后完成一个连通分量的遍历时 ，count++。

代码

用例: 点的个数+邻接矩阵

12
0 1 1 0 0 1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0 0
0 0 0 1 0 1 1 0 0 0 0 0 0
1 0 0 1 1 0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1 1
0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 1 0 0 1
0 0 0 0 0 0 0 0 0 1 0 1 0

结果：

3

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    private static int color[], map[][];
    private static Scanner in = new Scanner(System.in);
    private static int N, count;

    public static void main(String[] args) {
        N = in.nextInt();
        map = new int[N + 1][N + 1];
        color = new int[N + 1];
        Arrays.fill(color, -1);
        for (int i = 0; i <= N; i++) {
            for (int j = 0; j <= N; j++)
                map[i][j] = in.nextInt();
        }
        CC();
        System.out.println(count);
    }

    public static void CC() {
        for (int i = 0; i <= N; i++) {
            if (color[i] == -1) {
                dfs(i);
                count++;
            }
        }
    }
    private static void dfs(int i) {
        color[i] = count;
        for (int k = 0; k < map[i].length; k++)
            if (color[k] == -1 && map[i][k] == 1) dfs(k);
    }
}