红黑树
前言
以前在了解HashMap时得知JDK8的Map是用红黑树实现的（存储元素的链表达到一定长度后，会变为红黑树），而且网上还流传着面试手写红黑树的梗，数据结构课上也没交过这个
一、为什么要用红黑树
因为相较于普通的二叉搜索树，红黑树具有平衡性。这与AVL树相似，在增加或删除元素后可能会出现旋转的操作。 但是相较于AVL树严格的约束（左右子树的高度之差的绝对值最多为1），红黑树的平衡约束更为宽松，其旋转操作的时间复杂度为O(1)，而AVL树的旋转操作的时间复杂度为O(log n)。 因此在做增加、删除操作时可以选择红黑树，而在做搜索操作时选择AVL树（因为严格的平衡性，高度一般比红黑树低）。
二、定义
红黑树（Red Black Tree） 是一种自平衡二叉查找树。
三、性质
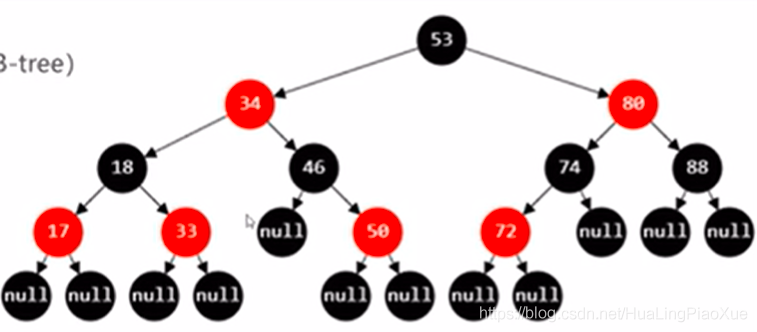
- 节点是红色或黑色
- 根节点必须是黑色
- 叶子节点（null节点）必须是黑色
- 红色节点的子节点都是黑色的，红色节点的父节点是黑色的
- 从根节点起到叶子节点的所有路径中，不能有两个连续的红色节点
- 从根节点起到叶子节点的所有路径中，黑色节点的个数都是相同的
为了方便起见，后面省略null节点
四、操作
1.搜索
同二叉搜索树一样，差不了多少，从根节点比大小，走分支
2.添加
添加操作比较复杂，情况比较多。
添加的节点本身都是红色，为了区别开来，这里都用粉红色代表新添加的节点。
2.1.添加到黑色节点
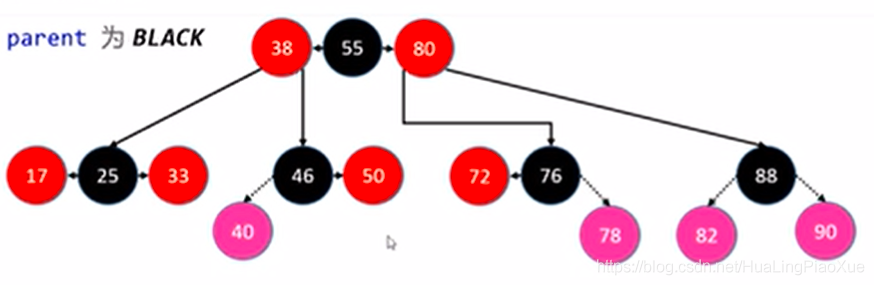这是最简单的一种情况，粉红色的为新添加的节点，其父节点为黑色，不违反性质4，所以不需要旋转。
2.2.添加到红色节点
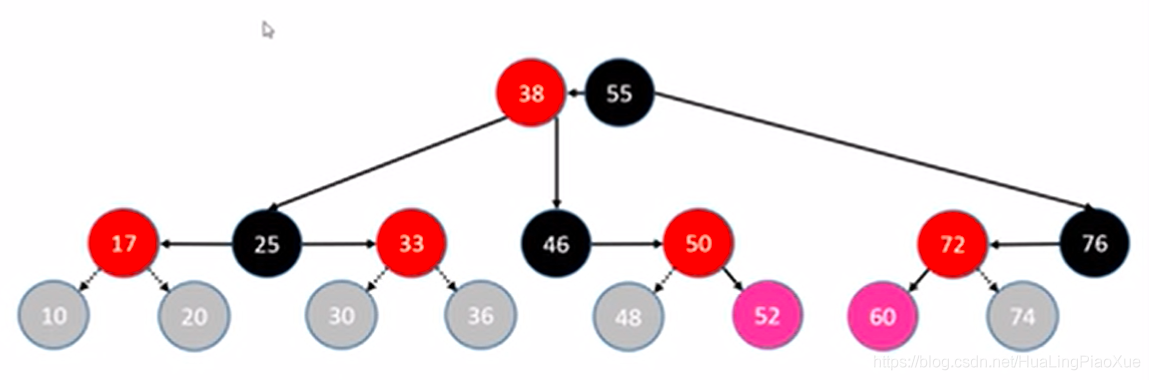出现了红色节点的子节点是红色的情况，违反性质4、5，所以需要旋转。
- LL型 uncle节点为黑
- RR型 uncle节点为黑
- LR型 uncle节点为黑
- RL型 uncle节点为黑
- LL型 uncle节点为红色
- RR型 uncle节点为红色
- LR型 uncle节点为红色
2.2.1.LL型 uncle节点为黑
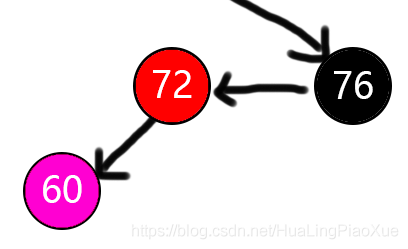
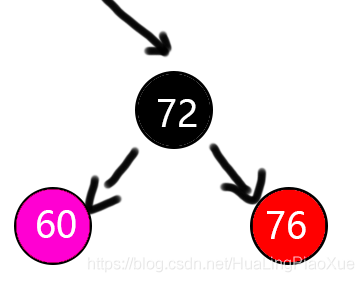
如图，新增节点60，是76左孩子的左孩子，这种类型被称之为LL型，显然LL型是不符合性质4的。 此时需要右旋，将72变黑，76变红，同时72变为76的父节点，即可满足性质4。 如果60有兄弟节点，则将其移动到祖节点76的下面。
2.2.2.RR型 uncle节点为黑
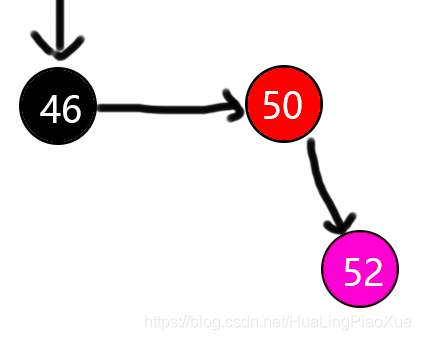
如图，新增节点52，是46右孩子的右孩子，这种类型被称之为RR型，显然RR型是不符合性质4的。 此时左旋，将50变黑，46变红，同时50变为46的父节点，即可满足性质4。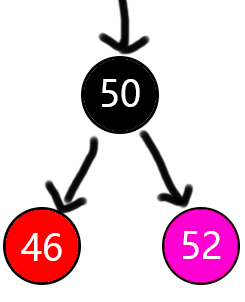 
2.2.3.LR型 uncle节点为黑
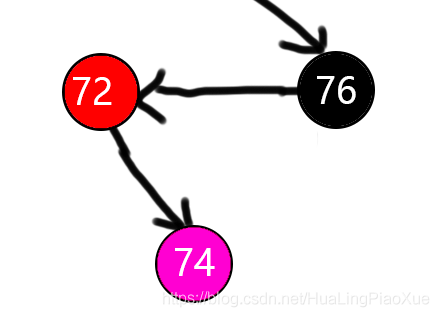
旋转后，新增的子节点74变为黑色，父节点和祖父节点变为红色作为74的子节点
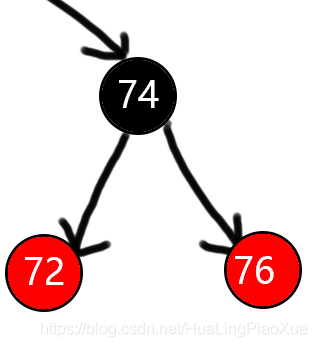
2.2.4.RL型 uncle节点为黑
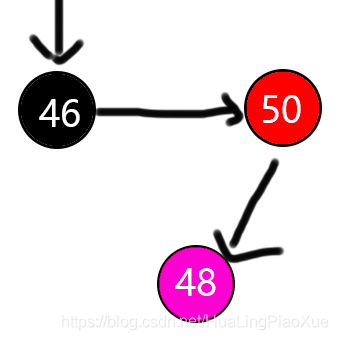
旋转后，新增的子节点48变为黑色，父节点和祖父节点变为红色作为74的子节点
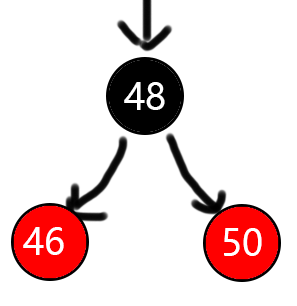
2.2.5.LL型 uncle节点为红色
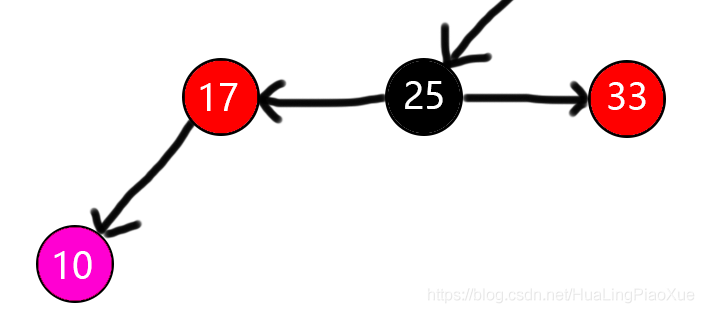
将父节点，叔节点变黑，祖节点变红，如下图：
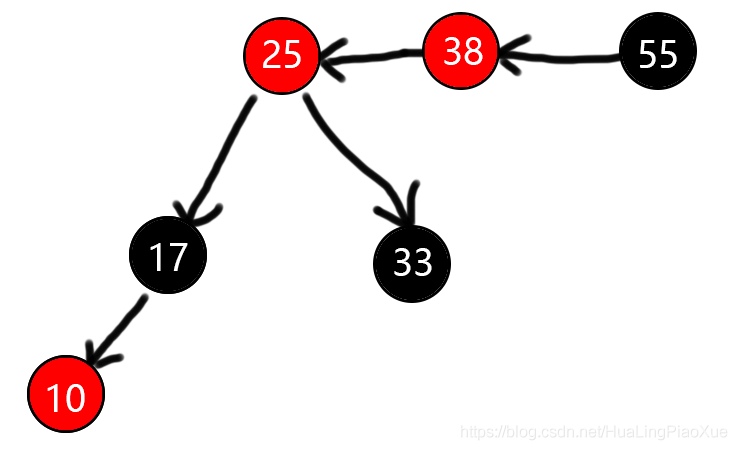
会发现，此时已然不符合性质4，但是25、38、55符合2.2.1的LL型，右旋即可。
2.2.6.RR型 uncle节点为红色
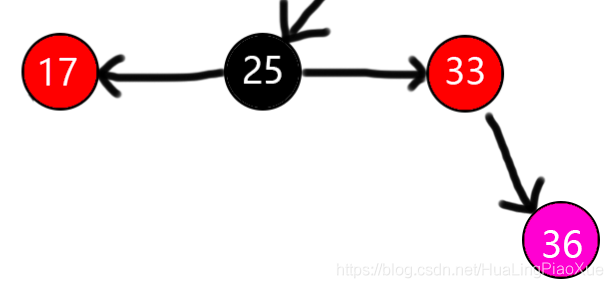
变色后
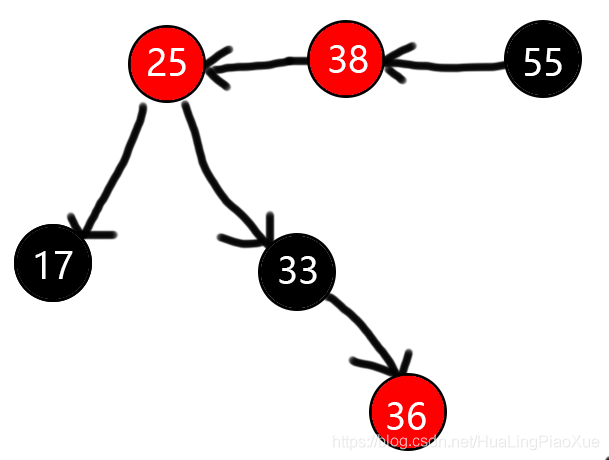
符合2.2.1的LL型，右旋即可
2.2.7.LR型 uncle节点为红色
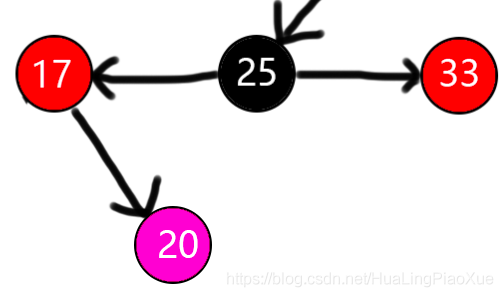
变色后：
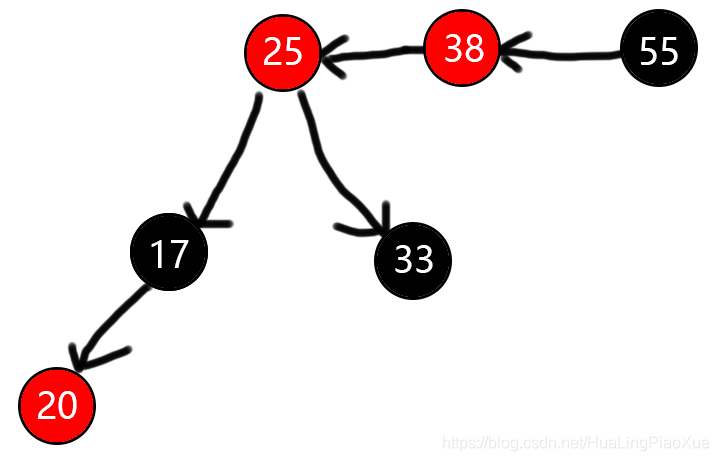
符合2.2.1的LL型，右旋即可
2.2.7.RL型 uncle节点为红色
......
3.删除
3.1 删除度为2的黑色节点
找该节点的前驱或后继替换掉该节点。
3.2 删除拥有一个红色子节点的黑色节点
找该节点的前驱或后继替换掉该节点，然后染黑。
3.3 删除度为0的黑色节点
3.3.1 兄弟节点是黑色且有红色子节点
删除该节点，然后旋转、染色。
3.3.2 兄弟节点是黑色且无红色子节点
将兄弟节点染成红色，父节点染成黑色。
3.4 删除红色节点
直接删除
。。。。。。。太麻烦了。。。。。。。。。。。。。。。。。。。。。。。。。。不想写了